BASI DI AERODINAMICA: IL TUBO DI VENTURI
Grazie allo scorso capitolo teorico, la definizione tecnica di flusso d’aria, possiamo spingerci oltre ed analizzare un capitolo fondamentale per la comprensione delle auto da corsa: il tubo di venturi.
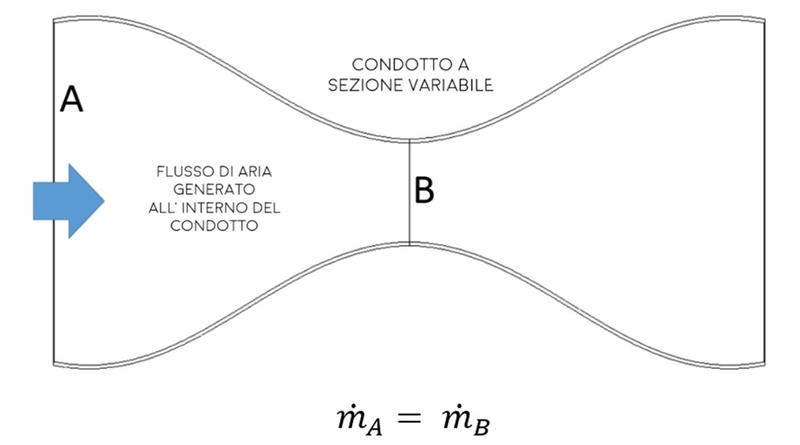
Come detto, il punto di partenza torna ad essere l’equazione dei flussi, di cui la spiegazione al seguente LINK. Essa, infatti può descrivere ogni tipo di corrente fluida, compresa quella che fluisce all’interno di un condotto a sezione variabile. Il tubo di Venturi, del resto, non è nient’altro che questo: un condotto a sezione variabile e al suo interno viene generata una corrente d’aria o di qualsiasi fluido si voglia considerare.
LE PRESSIONI INTERNE AL TUBO DI VENTURI
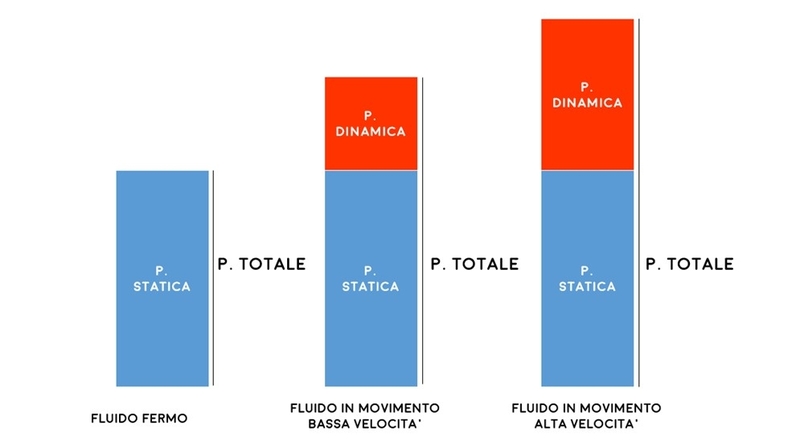
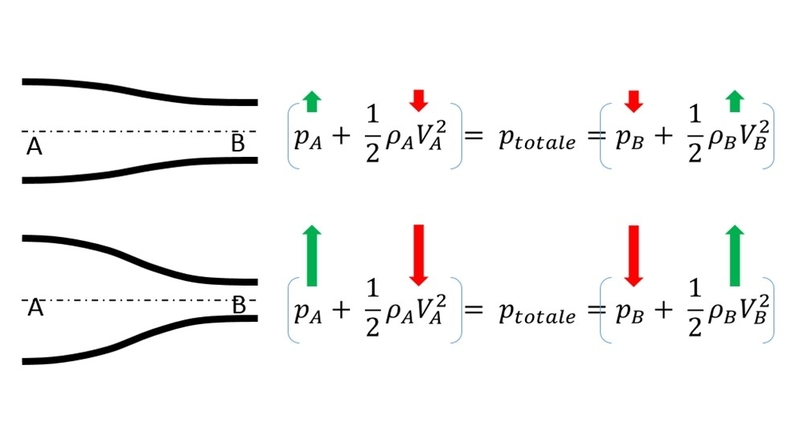
Il fluido che attraversa il tubo in questione possiede un suo valore di pressione totale che, in breve, rappresenta la somma tra la pressione statica e la pressione dinamica:
- La pressione dinamica è la componente di pressione di un fluido associata all’energia cinetica nel momento in cui questo fosse in movimento. Più la velocità del fluido cresce, maggiore sarà la percentuale di pressione sotto-forma di energia cinetica.
- La pressione statica è la pressione percepibile interna al fluido, sia esso in movimento, sia esso fermo. In sostanza, per mezzi di trasporto che si muovono nell’atmosfera, è quella riferita alla pressione ambiente.
Come detto, la pressione totale è la somma delle due componenti.
Nello schema precedente:
P° = pressione totale.
Ps = pressione statica.
Pd = pressione dinamica.
COMPORTAMENTO DEL FLUSSO DENTRO IL CONDOTTO
Di conseguenza parte della pressione totale si presenterebbe sotto forma di energia cinetica qualora il fluido fosse in movimento. Maggiore sarà la velocità raggiunta, maggiore sarà la quantità di pressione dinamica.
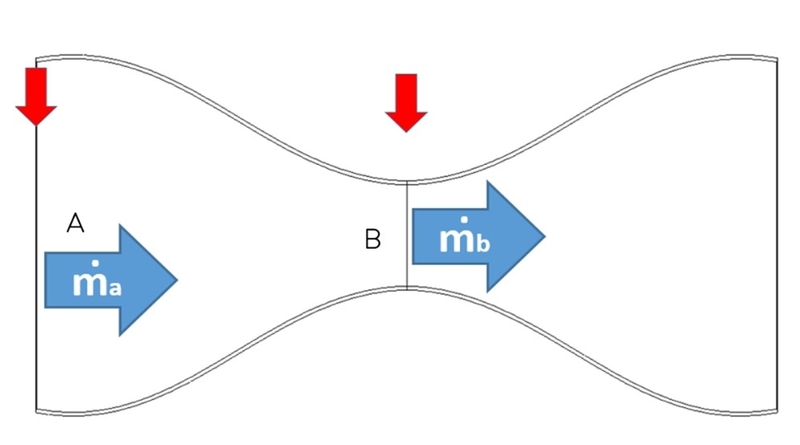
Vediamo l’immagine seguente: il flusso d’aria entra a sinistra tramite la sezione “A” e attraversa tutto il tubo fino a raggiungere l’uscita sul lato opposto del condotto. Il gas in ingresso ha assunto una pressione interna che corrisponde al valore statico e un valore di pressione dinamica legato alla velocità di scorrimento. La loro somma, la pressione totale, rimane costante una volta all’interno del tubo vista la mancanza di nuove aggiunte o sottrazioni di energia. Scorrendo, incontra un restringimento definito con la lettera “B”, che agisce sulla corrente modificandone le proprietà di pressione e densità.
Come?
Il meccanismo con cui il tubo di Venturi opera sul flusso è il seguente:
La lettera ṁ rappresenta la portata di fluido in termini di massa, la quale scorre ogni secondo all’interno del tubo. Il concetto è molto semplice. La stessa quantità di flusso entrante in “A” deve per forza passare anche in “B”: essendo un condotto chiuso, non possono scomparire le molecole tra A e B.
Ovviamente, tra le due sezioni in esame, qualcosa cambia: la larghezza del condotto non è uguale lungo il tubo e, proprio in B, il suo valore è minimo. Questo significa che la quantità di corrente che scorre attraverso A faticherebbe a fluire anche attraverso la strettoia, a meno che qualcosa non cambi.
CRESCITA DELLA VELOCITA’ INTERNA
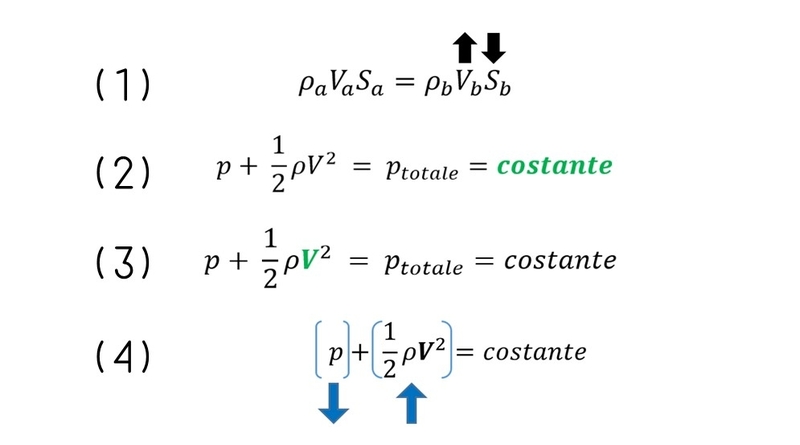
Per riuscire a passare tutte quante attraverso il punto più stretto del canale, le molecole devono accelerare. Solo in questo modo è possibile mantenere l’equilibrio tra le aree interne al condotto. La spiegazione numerica di seguito, grazie all’utilizzo dell’equazione di continuità (N.1 di seguito):
Si parli ora della variazione di pressione del fluido durante lo scorrimento dentro il canale a sezione variabile e per farlo, si consideri l’espressione matematica della pressione totale del fluido, equazioni 2 e 3 precedenti:
Il primo aspetto da discutere è il seguente: la somma tra pressione statica e pressione dinamica forniscono il valore di pressione totale che, come detto, rimane costante lungo tutto il tubo di Venturi. Non cambia perché non ci sono introduzioni di nuova energia che la possano far cambiare. Per questo motivo viene posta l’enfasi sul risultato “costante”.
Certo è che qualcosa, è stato detto, cambia: la velocità di scorrimento lungo le sezioni del tubo. Più il passaggio si restringe e più il flusso deve scorrere velocemente. Ciò pone l’attenzione su un altro fattore presente all’interno dell’equazione: La velocità. EQUAZIONE N.3 precedente.
RELAZIONE TRA VELOCITA’ DEL FLUSSO E PRESSIONE
come capito, la velocità aumenta o diminuisce a seconda della posizione delle molecole lungo il canale. A questo punto sorge spontaneo un ragionamento: se il valore della rapidità di scorrimento varia durante il passaggio delle molecole, ma il valore della pressione totale resta costante, cosa può diminuire per mantenere l’equilibrio all’interno delle equazioni viste in precedenza?
La pressione statica.
Lungo il condotto, a seconda della larghezza del passaggio nei vari punti, la velocità deve crescere o diminuire per permettere a tutte le molecole di passare mantenendo un certo equilibrio nella corrente fluida. Per farlo, come visibile nella figura seguente, la velocità aumenterà in prossimità delle strettoie a discapito della pressione interna al flusso e viceversa. Il risultato sarà tanto evidente quanto più il tubo mostrerà differenze tra le varie sezioni di passaggio.
E’ grazie a questo equilibrio che si ottiene la variazione di pressione statica interna al flusso: una parte di essa si converte in energia cinetica quando le molecole sono costrette ad accelerare, dovendo scorrere attraverso una strettoia.
Se le due sezioni sono molto differenti tra loro, il rapporto fornirà un risultato più elevato, indicando quindi una grande differenza anche tra le pressioni dinamiche. Viceversa, quando la sezione più stretta è molto simile a quella di ingresso, il flusso non è costretto a elevate accelerazioni.
CONSEGUENZE DEL CAMBIO DI VELOCITA’: IL CAMBIO DI PRESSIONE
Sapendo che all’aumentare della pressione dinamica si riduce quella statica, come introdotto ad inizio capitolo, il risultato principale è una riduzione di quest’ultima proprio nella strettoia. Il suo valore diminuisce tanto di più quanto più è alta la variazione tra le due sezioni in analisi. In conclusione, è possibile descrivere matematicamente come le due grandezze, pressione statica e pressione totale, attraverso la velocità del fluido, si regolino tra loro per dare un valore sempre costante, ma qual è il principio fisico alla base di quanto discusso fino ad ora?
DESCRIZIONE PRATICA DEL TUBO DI VENTURI
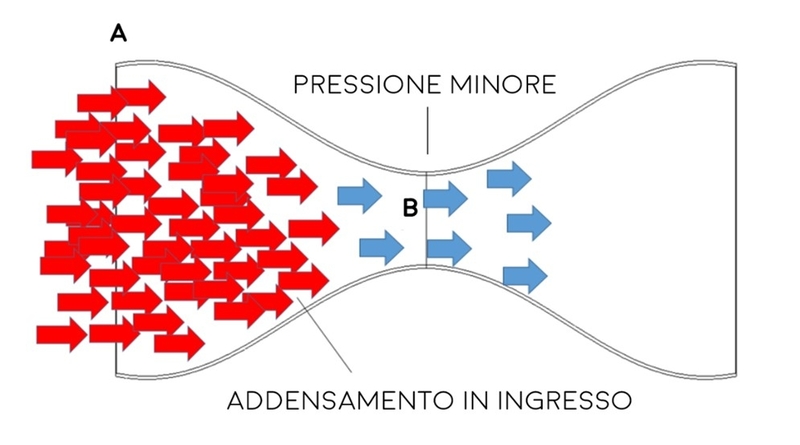
Si prenda ad esempio la sezione di condotto della figura seguente. La grande quantità di molecole in ingresso (sezione A) si addensa nella prima parte del condotto. Queste premono sulle particelle di aria già presenti nel punto di passaggio con area minore (sezione B) le quali, spinte, accelerano. Introducendo il termine “Spinta”, si intende che le molecole in ingresso mettono pressione e, nel farlo, si comprimono.
Premendo, generano un campo ad elevata pressione. Le molecole che si trovano in B, appena davanti a questa zona di alta pressione, vengono spinte grazie all’accumulo di particelle compresse che si trova all’ingresso del tubo e conseguentemente acquistano velocità. La logica conseguenza di questo effetto fisico è un calo di pressione nella strettoia, come ci si aspetterebbe da un insieme di particelle che si distanziano l’una dall’altra.
Si spiega cosi quanto descritto dall’equazione appena analizzata: la pressione scende nel punto in cui il flusso scorre più velocemente.
Per riassumere, sono tre gli aspetti principali del comportamento di un flusso all’interno del tubo di Venturi:
- Un flusso che accelera riduce la sua pressione statica.
- Un flusso che rallenta aumenta la sua pressione statica.
- Il flusso accelera maggiormente nel punto più stretto del condotto ed è più lento quando, in ingresso, la sezione di passaggio è più estesa.
Questo principio fisico è ritrovabile ovunque sulle vetture di F1. È facile rendersene conto, ad esempio, per il caso dei fondi piatti: anche questi elementi sono strutturati per funzionare sfruttando l’effetto Venturi. Avremo modo di analizzare questi ed altri elementi durante tutto l’anno di campionati. Inizieremo proprio con il prossimo articolo, descrivendo la motivazione che si cela dietro alla rastremazione delle pance laterali.
A presto, dall’ing. Alberto Aimar.