CAPIRE I CIRCUITI 3°Pt: CONFRONTO TRA RETTILINEI E CAMBI DI DIREZIONE
Per continuare a capire sempre meglio i circuiti e come l’aerodinamica si adatti ad essi, oggi affronteremo il rapporto tra lunghezza totale dei rettilinei e lunghezza totale dei cambi di direzione. LINK AL’ARTICOLO PRECEDENTE
Tale rapporto, la divisione tra la lunghezza totale dei tratti rettilinei e la lunghezza totale dei tratti curvilinei, fornisce il terzo grande fattore per capire e interpretare un circuito. Quanto fino ad ora spiegato negli altri capitoli, assieme all’analisi del parametro in corso, rappresenta un primo set di dati utili alla comprensione di una pista e delle caratteristiche che richiede alle vetture.
Di per se, anche questo indice, il rapporto delle lunghezze totali, non è così difficile da capire intuitivamente e non rappresenta altro che una divisione tra somme totali di lunghezze.
Ipotizziamo un circuito composto da due rettilinei, ciascuno di 400 metri, e un’estensione totale nominale di 1500 metri.
Il calcolo da effettuare è il seguente:
Il dato può partire da 0, in assenza di rettilinei (torniamo a ricordare il circuito di Nardò, in foto).
Lo stesso dato può teoricamente raggiungere valori anche molto elevati, ma un suo limite più o meno realistico si attesta a 1, massimo 1,5.
Per il circuito di Sandown in Australia, pista caratterizzata da lunghi rettilinei, il valore del rapporto vale 0,75.
Solo per poche eccezioni si sale più in alto. Un caso estremo, e più unico che raro, è il circuito di Ehra Lessien in Germania, circuito test volkswagen per le alte velocità. Un rettilinei da 8700metri, un simil rettilineo di lunghezza analoga, e due tratti curvilinei di lunghezza totale di 3000 metri circa, restituiscono un rapporto massimo di circa 5,8.
3 CIRCUITI A CONFRONTO
Visti alcuni esempi, torniamo a valutare il rapporto tra lunghezza massima dei rettilinei e lunghezza massima dei tratti curvilinei per i tre circuiti fino ad ora usati come esempio:
Monza: 0,77 (+17% rispetto all’Hungaroring).
Redbull ring: 0,77 (+17% rispetto all’Hungaroring).
Hungaro ring: 0,66.
Ecco quindi spiegato ciò che inizialmente, con il solo fattore di numero di curve su numero di rettilinei, LINK AL’ARTICOLO PRECEDENTE, non riuscivamo a spiegare. Monza aveva un valore paragonabile rispetto all’Hungaroring in termini di N curve su N rettilinei, ma sappiamo bene quanto i due circuiti vengano affrontati con carichi aerodinamici ben differenti (assai più elevati per il circuito ungherese). Bene, il rapporto in fase di studio durante il presente paragrafo è molto più alto per Monza, rispetto al caso ungherese: il 20% in più; i tratti rettilinei assumono una importanza maggiore per il circuito italiano. In questo senso, non è possibile sacrificare l’efficienza aerodinamica come avviene in Ungheria e, quindi, i profili alari devono essere molto meno inarcati.
Questo 20% circa diventa ancora più importante se pensiamo che il range di variazione del parametro in studio, e questo vale per la maggior parte dei circuiti, rimane sempre tra il minimo di 0,15 e il massimo di 0,77. Infatti, le eccezioni di circuiti che si avvicinano allo 0 non vengono praticamente mai usate per le competizioni, e solo casi rari come Nardò riescono ad assumere tale valore.
È un 20% che, se paragonato all’intervallo appena indicato, rappresenta circa il 25/30% almeno.
LA VARIABILITA’ DELLA LUNGHEZZA DEI RETTILINEI CHE CARATTERIZZA I CIRCUITI
Come per le curve, anche per i rettilinei non basta calcolare la lunghezza media. Serve sapere l’indice di variabilità, che è espresso tramite il calcolo della varianza.
Del resto, anche se non fatto in modo esplicito, calcolare la lunghezza media dei rettilinei diventa molto semplice, se guardiamo ai dati fino ad ora raccolti; dividendo la lunghezza totale di tutti i rettilinei sommati assieme per il loro numero, otteniamo esattamente il valore medio.
- Monza: 638 metri.
- Ungheria: 244 metri.
Prima di procedere, una osservazione: il calcolo di lunghezza media dei rettilinei appena svolto mostra ancor di più quanto (LINK AL’ARTICOLO PRECEDENTE), nonostante il numero di curve e rettilinei sia uguale per le due piste, in Ungheria i tratti dritti sono decisamente più corti e quindi caratterizzati da velocità assai minori. Banalmente, la macchina non ha spazio per raggiungere velocità elevate. Ciò permette un maggiore carico dinamico perché questo diventa decisamente inefficiente ad alte velocità; cosa che, come detto, non si verifica sull’Hungaroring.
L’IMPORTANZA DELLA VARIANZA SULLA LUNGHEZZA DEI RETTILINEI
Il capitolo in corso, però, non riguarda la lunghezza media dei rettilinei e quindi proseguiamo rispondendo al perché ci serve la varianza:
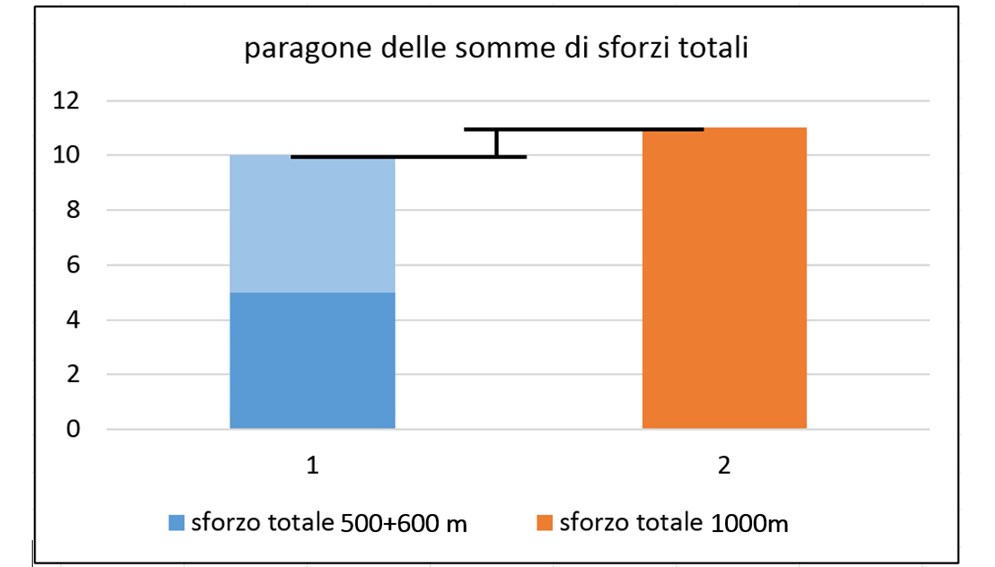
La risposta è molto più semplice di quel che potrebbe sembrare. Esattamente come per il caso dei raggi di curvatura, anche per i rettilinei bisogna sapere quanto questi siano simili tra loro. Se il valore medio di lunghezza dei rettifili su una pista con due tratti dritti è 550 metri, ma uno di questi è lungo 1000 metri e l’altro 100 metri, la pista si affronta in un modo; Se invece, con valore medio di 550 metri, i due rettilinei fossero di 500 e 600 metri rispettivamente, lo stesso valore andrebbe interpretato in modo completamente differente. Ecco perché:
- Qualora uno dei due rettilinei raggiungesse i 1000 metri, la penetrazione aerodinamica diventa fondamentale. Non si possono trascorrere tutti i secondi che servono a percorrerlo, accompagnati da un freno costante derivante da superfici aerodinamiche troppo sovradimensionate per il flusso in arrivo. La velocità persa sarebbe elevatissima.
- Se i due rettilinei fossero simili e di lunghezze molto vicine alla media, che nel nostro esempio assume un valore di 550 metri, l’auto non arriverebbe a velocità troppo alte e, comunque, non rimarrebbe sui rettilinei troppo tempo. Questo permetterebbe un aumento di carico aerodinamico, sapendo che la resistenza aerodinamica penalizzante sarebbe limitata.
La somma della resistenza totale sui due rettilinei da 500 e 600 metri risulta minore della somma della resistenza su un solo rettilineo da 1000 metri, visto che la resistenza aerodinamica cresce con il quadrato della velocità, la quale è molto più alta sul tratto dritto più lungo e dura più tempo.
Ecco quindi perché serve la varianza: il valore medio non basta per interpretare un percorso, come appena dimostrato.
LA VARIANZA SUI CIRCUITI DI MONZA, SPIELBERG E HUNGARORING
Vediamo come si calcola e come si deve interpretare tale aspetto. Lo si faccia con gli esempi fino ad ora mostrati, per garantire continuità alla trattazione.
il caso di Monza:
Varianza 0,18
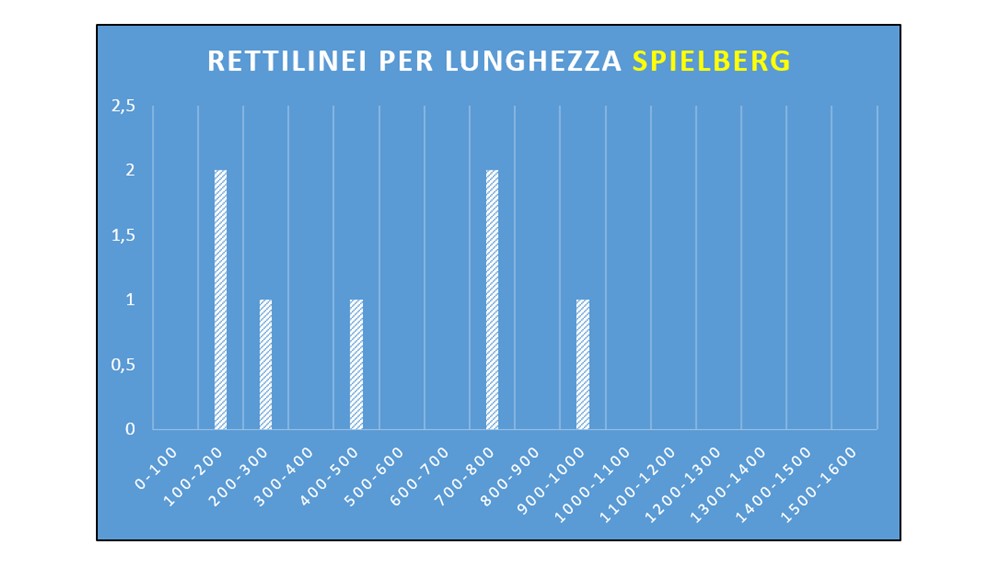
Il caso dello Spielberg:
Varianza: 0,10
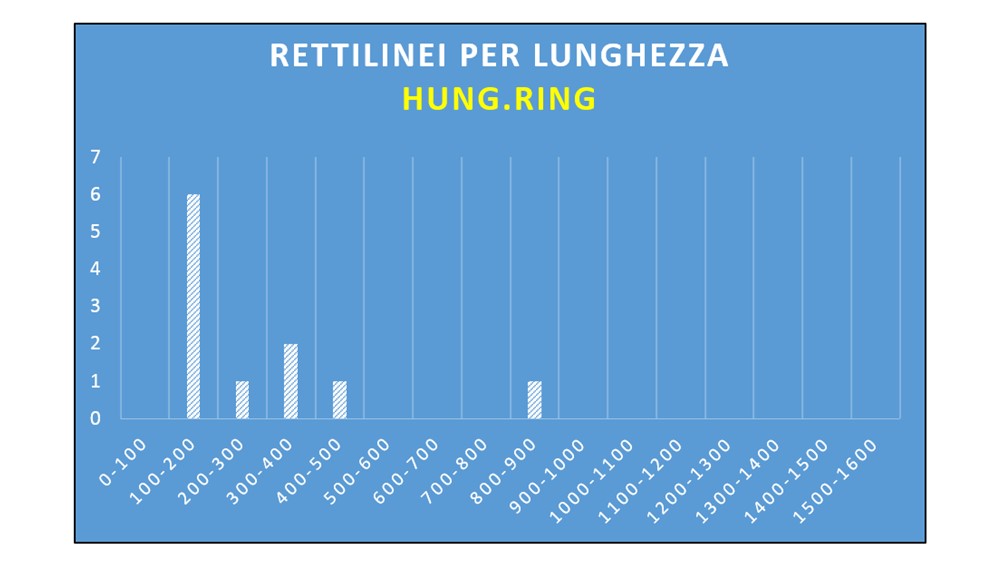
il caso dell’Hungaroring.
Varianza: 0,04
CONCLUSIONI
I rettilinei del circuito ungherese sono molto simili tra loro e, eccezion fatta per il rettifilo principale, l’80% di essi è compreso tra 100 e 400 metri. Cortissimi e da piena accelerazione; nessun farebbe obiezioni se decidessimo di caricare al massimo le superfici deportanti.
Monza, ma anche il RedBull Ring, mostrano variabilità ben più elevate e quindi bisogna fare attenzione a non sbagliare i calcoli: come detto prima, considerare la media va bene, ma si rischierebbe di penalizzare troppo i tratti veloci se non guardassimo anche alla varianza.
A presto dall’ing. Alberto Aimar.